 ((x)Fx
((x)Fx ∼Gx)
∼Gx)(b) (x)(( y)Fxy v Fyx)•∼Gx
y)Fxy v Fyx)•∼Gx
 y)Fxy v Fyx)•∼Gx
y)Fxy v Fyx)•∼Gx(c) (x)(Fxy (
( y)Fyx)(Fxy≡Fyx)
y)Fyx)(Fxy≡Fyx)
4.證明├A若且唯若 A
A
5.證明 (p
(p p)
p)
6.證明├( p
p (p
(p q))
q))
7.證明系統P的完全性定理(將所有需要的預備定理列出,但不必證明)
8.證明如果在系統P中加入聯立代換律,所成的系統的定理和系統P的定理相同。
9.證明下列完構式集合可滿足(任選其一)
 (
( y)Fyx)(Fxy≡Fyx)
y)Fyx)(Fxy≡Fyx)4.證明├A若且唯若
 A
A5.證明
 (p
(p p)
p)6.證明├(
 p
p (p
(p q))
q))7.證明系統P的完全性定理(將所有需要的預備定理列出,但不必證明)
8.證明如果在系統P中加入聯立代換律,所成的系統的定理和系統P的定理相同。
9.證明下列完構式集合可滿足(任選其一)
(a) {p,(x)Fx (
( y)Fy,Fx v Gxy}
y)Fy,Fx v Gxy}
 (
( y)Fy,Fx v Gxy}
y)Fy,Fx v Gxy}(b) {(x)( y)Fxy,Fxy v ∼Fyx,(x)Gx v (
y)Fxy,Fxy v ∼Fyx,(x)Gx v ( y) ∼Gy}
y) ∼Gy}
 y)Fxy,Fxy v ∼Fyx,(x)Gx v (
y)Fxy,Fxy v ∼Fyx,(x)Gx v ( y) ∼Gy}
y) ∼Gy}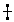 },而{
},而{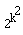 個。( )
個。( )