In what follows, we will first give a reconstruction of one of the commonsensical or semi-philosophical notions of possible world, namely, the view which identifies possible worlds with those worlds which are conceivable. After that, we are going to introduce an alternative way of characterizing a possible world which will be called "syntactical". We will begin with easier and naive cases, and move on to the more complicated and adequate ones. Hence this discussion will be presented in such a way that what we shall say in a latter stage of this discussion will be understood as a refinement of what we shall have said in an earlier stage.
2.Possible worlds in terms of conceivability
2.Possible worlds in terms of conceivability
It is commonplace for a philosopher to define a possible world in terms of conceivability. We may want to say that a world is possible if and only if it is conceivable. But this definition is so over-simplified that seems to convey little information. We may legitimately ask the questions: What kind of mental activity we refer to when we use the phrase 'to conceive'? Does it result from a process of careful logical survey, or is it a kind of intuitive meditation? More likely than not, to this question we will get an answer of the following sort: If we can conceive a possible world simply by meditation, fine; otherwise, go on to the logical calculation. This answer, however, add nothing to the clarification of the concept of the possible world. To see this, let us raise the following question: How many possible worlds are there all together? This question, though not an unambiguous one, as we shall see later, is nevertheless intuitively clear, or more appropriately speaking, not vague. As an advocator of the concept of conceivability, we may wish to answer that question in the following way. First of all, pick out a world W1 that is obviously possible. For the sake of convenience, let W1 be our world. Clearly it is a possible world, since actuality implies possibility. Then choose a certain basic feature (or if we like, but better avoid, quality), say ,of the world W1 .Imagine a world W2 which is exactly like W1 except where W1 has
,of the world W1 .Imagine a world W2 which is exactly like W1 except where W1 has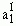 , W2 has a "slightly" different feature
, W2 has a "slightly" different feature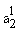 . Continue this process. In general, we have a world Wk which is exactly like all the world W1, W2…, Wk-1except that Wk has
. Continue this process. In general, we have a world Wk which is exactly like all the world W1, W2…, Wk-1except that Wk has 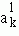 which is slightly different from any
which is slightly different from any 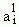 (i=1,2,…,k-1). Let us grant that "slight difference" is only a disquised name of a notion which can , in the final analysis, be precisely redefined, for example, in terms of mathematical functions. Hence, let us agree that the notion of "slight difference" gives a generating procedure which can be used to bring about a conceivable, and hence, a possible world from a set of already conceived worlds. Then, to the previous question we will most likely give an answer to the effect that there are infinitely many possible worlds, because we can make the above mentioned variation indefinitely. However, what we said above does not exhaust all the possible ways of variation in the application of our generating procedure. What we have outlined is a process of generating with respect to the variation on
(i=1,2,…,k-1). Let us grant that "slight difference" is only a disquised name of a notion which can , in the final analysis, be precisely redefined, for example, in terms of mathematical functions. Hence, let us agree that the notion of "slight difference" gives a generating procedure which can be used to bring about a conceivable, and hence, a possible world from a set of already conceived worlds. Then, to the previous question we will most likely give an answer to the effect that there are infinitely many possible worlds, because we can make the above mentioned variation indefinitely. However, what we said above does not exhaust all the possible ways of variation in the application of our generating procedure. What we have outlined is a process of generating with respect to the variation on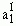 .We may vary on another feature, say
.We may vary on another feature, say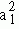 , too, and so on (where the variation may be similar or quite different). The question is : How many features, say
, too, and so on (where the variation may be similar or quite different). The question is : How many features, say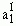 ,
,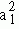 ,
,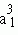 …, we may select or abstract from the world W1 to carry out our process of variation. There seems a sound reason to believe this word is a finite world no matter how huge it may be. And hence it seems quite safe to assume that the number of basic features we may arrive at is also finite, say n. Now, to calculate the total number of possible worlds, let us begin by looking at the following chart:
…, we may select or abstract from the world W1 to carry out our process of variation. There seems a sound reason to believe this word is a finite world no matter how huge it may be. And hence it seems quite safe to assume that the number of basic features we may arrive at is also finite, say n. Now, to calculate the total number of possible worlds, let us begin by looking at the following chart:
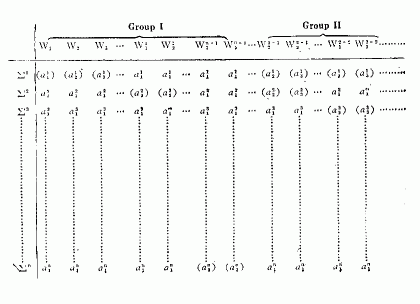
 to
to  are those n basic features of W1 subject to variation. For each feature there corresponds a procedure of variation. Hence we have n, not necessarily different, ways of variation. Let us call each of them, and hence each of the procedures of generating, Σi (i=1,2,…,n) . Group I in the chart indicates elliptically the possible worlds thus generated when exactly one generating procedure comes into operation. There are C(n,1), that is n, different ways of generating . Group II indicates similarly when exactly two such procedures are involved. In this case, we have C(n,2) different ways of generating. Likewise, we may have Group III,…, up to Group n in which all n procedures are put into work together. And in this case we have C(n,n), that is one, way of generating. In total, we have
are those n basic features of W1 subject to variation. For each feature there corresponds a procedure of variation. Hence we have n, not necessarily different, ways of variation. Let us call each of them, and hence each of the procedures of generating, Σi (i=1,2,…,n) . Group I in the chart indicates elliptically the possible worlds thus generated when exactly one generating procedure comes into operation. There are C(n,1), that is n, different ways of generating . Group II indicates similarly when exactly two such procedures are involved. In this case, we have C(n,2) different ways of generating. Likewise, we may have Group III,…, up to Group n in which all n procedures are put into work together. And in this case we have C(n,n), that is one, way of generating. In total, we have
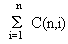
different ways of generating a set of possible worlds. And each set as we said before seems infinite. Now, suppose each generating procedure is precisely defined, and we have a way to order the possible worlds generated (e.g. to use diagonal method), we might arrive at a conclusion that the cardinality of each set is equal to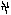
 . Therefore, the total number N(W) of possible worlds will be
. Therefore, the total number N(W) of possible worlds will be
(A)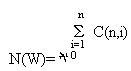
However, it should be emphasized that what formula (A) expresses is hardly anything other than a conjecture. Because, on the one hand, we based our analysis on such an obscure concept, viz, "basic feature in W1", and, one the other hand, we made, in our derivation, such strong suppositions like the assertions that each Σi can be well-defined and the generated possible worlds can be ordered in one-one fashion with the set of natural numbers.
 ,of the world W1 .Imagine a world W2 which is exactly like W1 except where W1 has
,of the world W1 .Imagine a world W2 which is exactly like W1 except where W1 has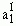 , W2 has a "slightly" different feature
, W2 has a "slightly" different feature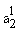 . Continue this process. In general, we have a world Wk which is exactly like all the world W1, W2…, Wk-1except that Wk has
. Continue this process. In general, we have a world Wk which is exactly like all the world W1, W2…, Wk-1except that Wk has 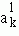 which is slightly different from any
which is slightly different from any 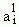 (i=1,2,…,k-1). Let us grant that "slight difference" is only a disquised name of a notion which can , in the final analysis, be precisely redefined, for example, in terms of mathematical functions. Hence, let us agree that the notion of "slight difference" gives a generating procedure which can be used to bring about a conceivable, and hence, a possible world from a set of already conceived worlds. Then, to the previous question we will most likely give an answer to the effect that there are infinitely many possible worlds, because we can make the above mentioned variation indefinitely. However, what we said above does not exhaust all the possible ways of variation in the application of our generating procedure. What we have outlined is a process of generating with respect to the variation on
(i=1,2,…,k-1). Let us grant that "slight difference" is only a disquised name of a notion which can , in the final analysis, be precisely redefined, for example, in terms of mathematical functions. Hence, let us agree that the notion of "slight difference" gives a generating procedure which can be used to bring about a conceivable, and hence, a possible world from a set of already conceived worlds. Then, to the previous question we will most likely give an answer to the effect that there are infinitely many possible worlds, because we can make the above mentioned variation indefinitely. However, what we said above does not exhaust all the possible ways of variation in the application of our generating procedure. What we have outlined is a process of generating with respect to the variation on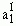 .We may vary on another feature, say
.We may vary on another feature, say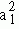 , too, and so on (where the variation may be similar or quite different). The question is : How many features, say
, too, and so on (where the variation may be similar or quite different). The question is : How many features, say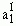 ,
,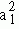 ,
,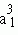 …, we may select or abstract from the world W1 to carry out our process of variation. There seems a sound reason to believe this word is a finite world no matter how huge it may be. And hence it seems quite safe to assume that the number of basic features we may arrive at is also finite, say n. Now, to calculate the total number of possible worlds, let us begin by looking at the following chart:
…, we may select or abstract from the world W1 to carry out our process of variation. There seems a sound reason to believe this word is a finite world no matter how huge it may be. And hence it seems quite safe to assume that the number of basic features we may arrive at is also finite, say n. Now, to calculate the total number of possible worlds, let us begin by looking at the following chart:
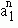 to
to 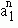 are those n basic features of W1 subject to variation. For each feature there corresponds a procedure of variation. Hence we have n, not necessarily different, ways of variation. Let us call each of them, and hence each of the procedures of generating, Σi (i=1,2,…,n) . Group I in the chart indicates elliptically the possible worlds thus generated when exactly one generating procedure comes into operation. There are C(n,1), that is n, different ways of generating . Group II indicates similarly when exactly two such procedures are involved. In this case, we have C(n,2) different ways of generating. Likewise, we may have Group III,…, up to Group n in which all n procedures are put into work together. And in this case we have C(n,n), that is one, way of generating. In total, we have
are those n basic features of W1 subject to variation. For each feature there corresponds a procedure of variation. Hence we have n, not necessarily different, ways of variation. Let us call each of them, and hence each of the procedures of generating, Σi (i=1,2,…,n) . Group I in the chart indicates elliptically the possible worlds thus generated when exactly one generating procedure comes into operation. There are C(n,1), that is n, different ways of generating . Group II indicates similarly when exactly two such procedures are involved. In this case, we have C(n,2) different ways of generating. Likewise, we may have Group III,…, up to Group n in which all n procedures are put into work together. And in this case we have C(n,n), that is one, way of generating. In total, we have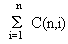
different ways of generating a set of possible worlds. And each set as we said before seems infinite. Now, suppose each generating procedure is precisely defined, and we have a way to order the possible worlds generated (e.g. to use diagonal method), we might arrive at a conclusion that the cardinality of each set is equal to
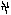
 . Therefore, the total number N(W) of possible worlds will be
. Therefore, the total number N(W) of possible worlds will be(A)
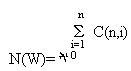
However, it should be emphasized that what formula (A) expresses is hardly anything other than a conjecture. Because, on the one hand, we based our analysis on such an obscure concept, viz, "basic feature in W1", and, one the other hand, we made, in our derivation, such strong suppositions like the assertions that each Σi can be well-defined and the generated possible worlds can be ordered in one-one fashion with the set of natural numbers.
To make matters even worse, consider the following questions: (1) What is a basic feature of W1? Are those n basic features we assumed mutually independent? How do we determine that featureαis independent of feature β other than the ad hoc justification to the effect that βis independent ofα if βis not generated fromα under certain generating procedure Σi. (2)How do we know that there are no two generating proceduresΣi andΣj such that certain step they may generate αi and αj, respectively, which turn out to be two conflicting , or contradicting, features. To put the question in another way, how do we know that the features thus generated under different procedures will not cancel each other, and thus decrease the number of possible worlds expressed in (A). (3) How to answer, either positively or negatively, the question whether these n features are sufficient to produce every conceivable feature. For example, are we sure that unicorns will be in at least one of our possible worlds? (4) In formula (A) what we have is the number of possible worlds of a certain kind, namely, those with n basic features. What justification we might have in making such supposition? Of course, we began with our world because we wanted to make sure that we worked on an obviously possible world. But why not just arbitrarily begin, say, with any number k (k=1,2,3,…), not necessarily finite, of basic features? Is it not equally easy for us to conceive a possible world with only one basic feature, or with only two basic features, or…, or with infinitely many basic features? Why not revise (A) to read as follows:
(B)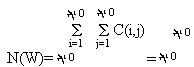
where we assume the infinitely many basic features are again denumerable. (5) Why we do not add in each of formulae (A) and (B) another possible world, namely, the empty world , a world in which there is no feature whatsover. Is it not a world easily conceivable?
(B)
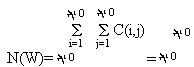
where we assume the infinitely many basic features are again denumerable. (5) Why we do not add in each of formulae (A) and (B) another possible world, namely, the empty world , a world in which there is no feature whatsover. Is it not a world easily conceivable?
We will make no attempt to answer these questions. Let them simply be some of the indications showing how ambiguous and vague our ordinary conception of the possible world in terms of conceivability could be.
3.Toward a syntactical approach.
3.Toward a syntactical approach.
Let us agree that we know what by a 'state-of-affairs'. Let us say that a world is composed of, or can be identified by, a class of states-of-affairs. In a world W, a state-of-affairs s either subsists or does not subsist. We will call it the subsistence value of s in W. Let '1' denotes the subsistence value subsistence and '0' denotes the subsistence value non-subsistence.
Consider, first of all, the worlds in which no state-of-affairs is involved. There is only one such world, namely, the empty world. Consider, secondly, the worlds in which only one state-of-affairs is involved, there are two of them. Similarily, there are four worlds all together in which two states-of-affairs are involved, and so on. In general, there are 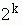 worlds in which k states-of-affairs can be said to be either subsistent or not subsistent. Observe the following chart, we can see that with respect to a fix state-of-affairs each time we introduce a new state-of-affairs, we split up each of the already obtained worlds in two:
worlds in which k states-of-affairs can be said to be either subsistent or not subsistent. Observe the following chart, we can see that with respect to a fix state-of-affairs each time we introduce a new state-of-affairs, we split up each of the already obtained worlds in two:
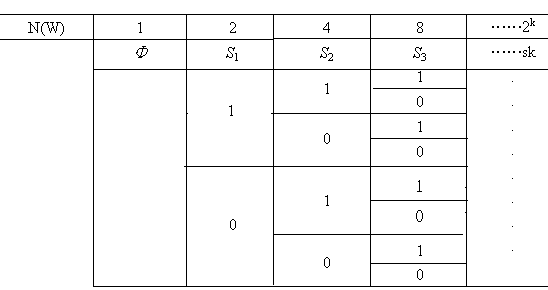
or, if we like, we may represent the list of possible worlds with respect to a state-of-affairs, say s1, in the following way. Let 'si'means "si has the value l" and ' i ' means "sI has the value O". Then we have the following:
i ' means "sI has the value O". Then we have the following:
{ }=Φ
{s1}, { }
{s1,s2},{s1, 2 },{
2 },{ 1,s2}{
1,s2}{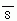 1,
1, 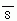 2}
2}
{s1,s2,s3,……sk}, {s1,s2,s3,……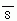 k },……, {
k },……, {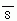 1,
1,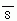 2,
2,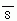 3,……
3,……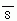 k}
k}
where each set stands for a possible world. From this, it is easy to see the total number of possible worlds, namely,
(C)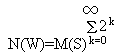
where M(S) is the supposed number of states-of-affairs. Note that in formula (C) we tantatively assumed that there are infinitely many state-of-affairs to be introduced, without saying which type of infinity we had in mind (while in formula (A) and (B) we assumed the smallest infinity).
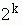 worlds in which k states-of-affairs can be said to be either subsistent or not subsistent. Observe the following chart, we can see that with respect to a fix state-of-affairs each time we introduce a new state-of-affairs, we split up each of the already obtained worlds in two:
worlds in which k states-of-affairs can be said to be either subsistent or not subsistent. Observe the following chart, we can see that with respect to a fix state-of-affairs each time we introduce a new state-of-affairs, we split up each of the already obtained worlds in two:
or, if we like, we may represent the list of possible worlds with respect to a state-of-affairs, say s1, in the following way. Let 'si'means "si has the value l" and '
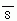 i ' means "sI has the value O". Then we have the following:
i ' means "sI has the value O". Then we have the following:{ }=Φ
{s1}, { }
{s1,s2},{s1,
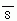 2 },{
2 },{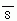 1,s2}{
1,s2}{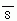 1,
1, 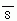 2}
2}{s1,s2,s3,……sk}, {s1,s2,s3,……
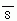 k },……, {
k },……, {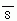 1,
1,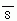 2,
2,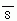 3,……
3,……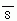 k}
k}where each set stands for a possible world. From this, it is easy to see the total number of possible worlds, namely,
(C)
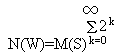
where M(S) is the supposed number of states-of-affairs. Note that in formula (C) we tantatively assumed that there are infinitely many state-of-affairs to be introduced, without saying which type of infinity we had in mind (while in formula (A) and (B) we assumed the smallest infinity).
Instead of talking about states-of-affairs, let us now take statements as their substituents. However, most of what we have said about states-of-affairs can be reformulated in terms of statements. Because it is commonly maintained that a statement can be used to enpress a state-of-affairs. For instance, the choice of no statement depicts the empty world while a choice of two statements exhibits one of four possible worlds. For the sake of convenience, we may use the standard truth table in propositional logic to indicate the number and expose the "propositional constituents" of the possible worlds with respect to certain statements, say a1, a2,am. For example, the following table shows that out of two statements a1 and a2, we have four possible worlds.
In addition, row one, i.e., (1)depicts a world in which both a1 and a2 hold. Likewise, row three, i.e., (3) is a world in which a2 holds but a1 fails to be true. Unlike the states-of-affairs, we can easily prove that out of finite number of basic linguistic elements, say alphabetical letters, the number of statements we can construct is infinitely many. And, furthermore, this infinity is the smallest one, namely, denumerable. Hence, it is readily seen that the total umber of possible worlds generated in this way will be the following:
(D)
| a1 | a2 | |
| t | t | (1) |
| t | f | (2) |
| f | t | (3) |
| f | f | (4) |
In addition, row one, i.e., (1)depicts a world in which both a1 and a2 hold. Likewise, row three, i.e., (3) is a world in which a2 holds but a1 fails to be true. Unlike the states-of-affairs, we can easily prove that out of finite number of basic linguistic elements, say alphabetical letters, the number of statements we can construct is infinitely many. And, furthermore, this infinity is the smallest one, namely, denumerable. Hence, it is readily seen that the total umber of possible worlds generated in this way will be the following:
(D)

One question which remains suppressed so far may at this point be brought up onto the surface. Namely, how do we know that in our list of denumerably many statements, no two of them are contradicting to each other, hence they might decrease the number of possible worlds? The first half of the question is legitimate while the second half may not be. We did not devise a logic filter to sort out a set of mutually consistent statements. Nevertheless, it is not hard to show that after we eliminate those statements which may threaten a contradiction to our list of statements, we still have denumerably many mutually consistent statements left behind. Hence, the total number of possible worlds is in no way affected. However, this question does remind us that in our description of how possible worlds may be accounted for by means of a set of statements, we have to make sure we arrive at a mutually consistent set each time; otherwise, the set is not qualified to represent a possible world. Similar remarks can be made to the depiction of possible worlds in terms of states-of-affairs. But in this case things become much less clear whether there are denumerably many "mutually consistent" (whatever this means) states-of-affairs or not, unless we make very strong claim that to each statement there corresponds one and only one state-of-affairs.
4.Denumerable statements out of a finite dictionary
4.Denumerable statements out of a finite dictionary
In last section we stated without a proof the fact that out of a finite class of symbols we can form a denumerably many statements. In this section, we will give a proof of that thesis. And, after that has been done, we will outline, in the next section, an alternative way of looking at possible worlds by way of syntactical characterization. Now, the first objective.
Let D be a finite dictionary consisting of k symbols b1, b2,…bk. An expression E is a finite string α1α2α3 …αt of symbols, not necessarily distinct, fromb1,b2,…,bk . Let f be a function which maps {b1, b2,…,bk} onto the first kth primes in the natural order. That is,
f(b1)=2,f(b2)=3, f(b3 )=5,…
and let f(Φ)=1 (in order to account for the blank). Define the Godel number (GN) of an expression E=α1α2α3…αu as
GN(E)=f(α1)•(α2)•f(α3)•…•(αu) namely, the product of the images ofα1, α2,…, αu under f. We know that each expression, under this definition, has a unique Godel number. And, furthermore, by the unique factorization theorem in arithmetic, to each Godel number, there corresponds a unique set of symbols, and, with respect to a definite Godel number, this set of symbols is finite. Now, order the expressions of D as follows. Let E1 and E2 be any arbitrary expressions such that
E1=α1α2α3…αs E2=β1β2β3…βt
E1 precedes E2 if and only if GN(E1)〈GN(E2), or
f(α1)〈f(β1) & GN(E1)=GN(E2), or
f(α2)〈f(β2&f(β1)=f(β1)&GN(E1)=GN(E2), or …,or
f(αn)〈f(βn)&f(α1)=f(β1)&…&f(βn-1) =f(βn-1)&GN(E1)=GN(E2), or
…………
This is a set of rule will order every expression of D. Once the order is established we put the set of expressions of D into a one-one correspondence with the set of positive integers. This show that the number of expressions of D is exactly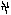 0. namely, denumerably many.
0. namely, denumerably many.
f(b1)=2,f(b
and let f(Φ)=1 (in order to account for the blank). Define the Godel number (GN) of an expression E=α1α2α3…αu as
GN(E)=f(α1)•(α2)•f(α3)•…•(αu) namely, the product of the images ofα1, α2,…, αu under f. We know that each expression, under this definition, has a unique Godel number. And, furthermore, by the unique factorization theorem in arithmetic, to each Godel number, there corresponds a unique set of symbols, and, with respect to a definite Godel number, this set of symbols is finite. Now, order the expressions of D as follows. Let E1 and E2 be any arbitrary expressions such that
E1=α1α2α3…αs E2=β1β2β3…βt
E1 precedes E2 if and only if GN(E1)〈GN(E2), or
f(α1)〈f(β1) & GN(E1)=GN(E2), or
f(α2)〈f(β2&f(β1)=f(β1)&GN(E1)=GN(E2), or …,or
f(αn)〈f(βn)&f(α1)=f(β1)&…&f(βn-1) =f(βn-1)&GN(E1)=GN(E2), or
…………
This is a set of rule will order every expression of D. Once the order is established we put the set of expressions of D into a one-one correspondence with the set of positive integers. This show that the number of expressions of D is exactly
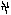 0. namely, denumerably many.
0. namely, denumerably many.Now, among the set of expressions there are some which will be called sentences or statements according to certain set of grammatical rules. We can also show that the cardinality of the set of statements is also 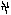 0. However, in order to prove this, we need a set of rules which can effectively sort out an expression which is grammatical from others which are not. But since we want our discussion outlined here to be as general as possible, we will not specify such a set of rules. Nevertheless, a special type of proof to the aforesaid effect can be outlined as follows:
0. However, in order to prove this, we need a set of rules which can effectively sort out an expression which is grammatical from others which are not. But since we want our discussion outlined here to be as general as possible, we will not specify such a set of rules. Nevertheless, a special type of proof to the aforesaid effect can be outlined as follows:
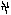 0. However, in order to prove this, we need a set of rules which can effectively sort out an expression which is grammatical from others which are not. But since we want our discussion outlined here to be as general as possible, we will not specify such a set of rules. Nevertheless, a special type of proof to the aforesaid effect can be outlined as follows:
0. However, in order to prove this, we need a set of rules which can effectively sort out an expression which is grammatical from others which are not. But since we want our discussion outlined here to be as general as possible, we will not specify such a set of rules. Nevertheless, a special type of proof to the aforesaid effect can be outlined as follows:Hand pick a statement of a particular type, call it S. Show that if one of the constituents of S is replaced by another subexpression of the same type, then the resulting expression S1 is also a statement. Show, further, that in our language we have an infinite supply of sub-expressions of that type. Hence, we can generate infinitely many statements from S. This infinity must be denumerable. Now, since the expressions of which the class of statements is a proper subclass is denumerably many, and the class of statements generated from S which is a proper subclass of the class of statements is also denumerable; it follows that the class of statements must also be denumerable.
Likewise, we can also show that the mutually consistent class of statements also has 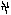 0 as its cardinality. Simply think of a set of rules by which we can add an additional statement to an already known consistent class of statements and thus to render a larger consistent class of statements. Since we can easily find a unit class of statements which is consistent, by mathematical induction together with the fact we just arrived at, namely there are denumerably many statements, we can show that the class of mutually consistent statements is also denumerable. Of course, this is only an outline, we need both a set of grammatical rules and a set of logical rules to fully carry out the proof.
0 as its cardinality. Simply think of a set of rules by which we can add an additional statement to an already known consistent class of statements and thus to render a larger consistent class of statements. Since we can easily find a unit class of statements which is consistent, by mathematical induction together with the fact we just arrived at, namely there are denumerably many statements, we can show that the class of mutually consistent statements is also denumerable. Of course, this is only an outline, we need both a set of grammatical rules and a set of logical rules to fully carry out the proof.
5.A second syntactical characterization
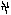 0 as its cardinality. Simply think of a set of rules by which we can add an additional statement to an already known consistent class of statements and thus to render a larger consistent class of statements. Since we can easily find a unit class of statements which is consistent, by mathematical induction together with the fact we just arrived at, namely there are denumerably many statements, we can show that the class of mutually consistent statements is also denumerable. Of course, this is only an outline, we need both a set of grammatical rules and a set of logical rules to fully carry out the proof.
0 as its cardinality. Simply think of a set of rules by which we can add an additional statement to an already known consistent class of statements and thus to render a larger consistent class of statements. Since we can easily find a unit class of statements which is consistent, by mathematical induction together with the fact we just arrived at, namely there are denumerably many statements, we can show that the class of mutually consistent statements is also denumerable. Of course, this is only an outline, we need both a set of grammatical rules and a set of logical rules to fully carry out the proof.5.A second syntactical characterization
Because of the reason which will be explained presently, the first syntactical characterization of possible worlds outlined in section 3 may turn out to be not quite satisfactory. As we recall, in the process of generating possible worlds, each time we take another statement into consideration, we split each of the already obtained world into two worlds. For instance, if we have{a1, a2}as representing a possible world, then a third statement a3 will make it split into the following two worlds ,i.e., {a1, a2, 3.} Now, a question may arise, as we indicated before, as to how we can be assured of the fact that these two sets are in fact representing two possible worlds without running into contradiction. For instance, if a3 is conflicting with a1, then {a1, a2 ,
3.} Now, a question may arise, as we indicated before, as to how we can be assured of the fact that these two sets are in fact representing two possible worlds without running into contradiction. For instance, if a3 is conflicting with a1, then {a1, a2 , 3}is not a possible world, though {a1, a2, a3}may well be. Hence, if we use the first syntactical method to generate the possible worlds, we face with a dilemma. Either we may include some impossible worlds to our list of possible worlds, or we have to make a supposition that all statements under consideration are mutually consistent. The latter is certainly too strong a supposition we wish to make. Hence, what we could do is most likely to try to find a way out of the first horn of the dilemma. In order to do this, we may develop a procedure serving as a logical de-contradictioner at some point in the generating process. For instance, using standard truth tables we are able to eliminate all the impossible worlds on truth functional level. But possible worlds are not exclusively in terms of truth functions. Hence, the problem has to be solved case by case.
3}is not a possible world, though {a1, a2, a3}may well be. Hence, if we use the first syntactical method to generate the possible worlds, we face with a dilemma. Either we may include some impossible worlds to our list of possible worlds, or we have to make a supposition that all statements under consideration are mutually consistent. The latter is certainly too strong a supposition we wish to make. Hence, what we could do is most likely to try to find a way out of the first horn of the dilemma. In order to do this, we may develop a procedure serving as a logical de-contradictioner at some point in the generating process. For instance, using standard truth tables we are able to eliminate all the impossible worlds on truth functional level. But possible worlds are not exclusively in terms of truth functions. Hence, the problem has to be solved case by case.
 3.} Now, a question may arise, as we indicated before, as to how we can be assured of the fact that these two sets are in fact representing two possible worlds without running into contradiction. For instance, if a3 is conflicting with a1, then {a1, a2 ,
3.} Now, a question may arise, as we indicated before, as to how we can be assured of the fact that these two sets are in fact representing two possible worlds without running into contradiction. For instance, if a3 is conflicting with a1, then {a1, a2 , 3}is not a possible world, though {a1, a2, a3}may well be. Hence, if we use the first syntactical method to generate the possible worlds, we face with a dilemma. Either we may include some impossible worlds to our list of possible worlds, or we have to make a supposition that all statements under consideration are mutually consistent. The latter is certainly too strong a supposition we wish to make. Hence, what we could do is most likely to try to find a way out of the first horn of the dilemma. In order to do this, we may develop a procedure serving as a logical de-contradictioner at some point in the generating process. For instance, using standard truth tables we are able to eliminate all the impossible worlds on truth functional level. But possible worlds are not exclusively in terms of truth functions. Hence, the problem has to be solved case by case.
3}is not a possible world, though {a1, a2, a3}may well be. Hence, if we use the first syntactical method to generate the possible worlds, we face with a dilemma. Either we may include some impossible worlds to our list of possible worlds, or we have to make a supposition that all statements under consideration are mutually consistent. The latter is certainly too strong a supposition we wish to make. Hence, what we could do is most likely to try to find a way out of the first horn of the dilemma. In order to do this, we may develop a procedure serving as a logical de-contradictioner at some point in the generating process. For instance, using standard truth tables we are able to eliminate all the impossible worlds on truth functional level. But possible worlds are not exclusively in terms of truth functions. Hence, the problem has to be solved case by case.The second syntactical approach we want to present here is by no means immune from this difficulty, and may be some additional difficulties, too. Nevertheless, in some cases, or with respect to certain types of langes, we might find it easier, or more convenient, to follow. The cornerstone of this method is the thesis that a consistent class of statements can be extended to a maximally consistent class. As we know, this thesis is true both in propositional logic and quantification theory. Whether it holds in any other more comprehensive language remains to be proved. But our outline is done on the presupposition that it can be shown to hold in the language we are talking about.
We know from last section that we can order the statements of a language in a linear manner. After this is done, pick up the first statement, S1, if it is not self-contradictory, clearly {S1} is a consistent class. Extend it to a maximally consistent class,Δ1. Pick up the second statement, S2, follow the same procedure, and so on. Consequently, we will obtain a set ofΔ's. Let us call them
Γ1, Γ2,…,Γn,…
respectively, where eachΓ1 is a Δj for some integers i and j, not necessarily differnent. Clearly the set ofΓ's is denumerably many (there may be repetitions among them), because we have denumerably many non-contradictory statements to begin with. In order to obtain every possible consistent class, let us take the power set of each setΓi. We may say that each member of the power set of eachΓi depicts a possible world, for each is obviously a consistent class. But some of them are repetitions of others. For instance, the empty set is encountered each time in the power set of eachΓi. Similarly, for a set with cardinality k (k≧1), there will be other k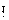 -1 repetitions somewhere in our list. E.g.,{Si, Sj,Sk} is the same set as {Si,Sk,Sj},{Sj,Sk,Si},{Sj,Si,Sk},{Sk,Si,Sj}, and {Sk,Sj,Si}. In view of these repititions, we know that the power set of each Γi contains less than or equal to 2
-1 repetitions somewhere in our list. E.g.,{Si, Sj,Sk} is the same set as {Si,Sk,Sj},{Sj,Sk,Si},{Sj,Si,Sk},{Sk,Si,Sj}, and {Sk,Sj,Si}. In view of these repititions, we know that the power set of each Γi contains less than or equal to 2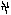 0 elements each of which representing a possible world. Hence, the total number of possible worlds is less than or equal to the total number of the elements of all power sets of Γ1, Γ2,…That is,
0 elements each of which representing a possible world. Hence, the total number of possible worlds is less than or equal to the total number of the elements of all power sets of Γ1, Γ2,…That is,

(E)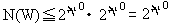
But since we have denumerably many Γ's , each of which containing at least one subset not equivalent to any subset of any other Γ. And since each such subset is taken to represent a possible world, we have
(F) N(W)≧2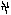 0
0
(E) and (F) together entail
(G) N(W)=2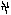 0
0
Compare (G) with (D) in section 3. Clearly . Therefore, we must say that if our inferences are all correct, then we have arrived at two separate syntactical notions of possible world.
. Therefore, we must say that if our inferences are all correct, then we have arrived at two separate syntactical notions of possible world.
6.A pragmatical supplement.
Γ1, Γ2,…,Γn,…
respectively, where eachΓ1 is a Δj for some integers i and j, not necessarily differnent. Clearly the set ofΓ's is denumerably many (there may be repetitions among them), because we have denumerably many non-contradictory statements to begin with. In order to obtain every possible consistent class, let us take the power set of each setΓi. We may say that each member of the power set of eachΓi depicts a possible world, for each is obviously a consistent class. But some of them are repetitions of others. For instance, the empty set is encountered each time in the power set of eachΓi. Similarly, for a set with cardinality k (k≧1), there will be other k
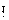 -1 repetitions somewhere in our list. E.g.,{Si, Sj,Sk} is the same set as {Si,Sk,Sj},{Sj,Sk,Si},{Sj,Si,Sk},{Sk,Si,Sj}, and {Sk,Sj,Si}. In view of these repititions, we know that the power set of each Γi contains less than or equal to 2
-1 repetitions somewhere in our list. E.g.,{Si, Sj,Sk} is the same set as {Si,Sk,Sj},{Sj,Sk,Si},{Sj,Si,Sk},{Sk,Si,Sj}, and {Sk,Sj,Si}. In view of these repititions, we know that the power set of each Γi contains less than or equal to 2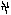 0 elements each of which representing a possible world. Hence, the total number of possible worlds is less than or equal to the total number of the elements of all power sets of Γ1, Γ2,…That is,
0 elements each of which representing a possible world. Hence, the total number of possible worlds is less than or equal to the total number of the elements of all power sets of Γ1, Γ2,…That is,
(E)
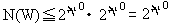
But since we have denumerably many Γ's , each of which containing at least one subset not equivalent to any subset of any other Γ. And since each such subset is taken to represent a possible world, we have
(F) N(W)≧2
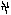 0
0 (E) and (F) together entail
(G) N(W)=2
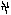 0
0Compare (G) with (D) in section 3. Clearly
 . Therefore, we must say that if our inferences are all correct, then we have arrived at two separate syntactical notions of possible world.
. Therefore, we must say that if our inferences are all correct, then we have arrived at two separate syntactical notions of possible world.6.A pragmatical supplement.
When we want to apply the notion of possible world to cope with other problems, our syntactical characterization may not appear to be adequate at all times. As an illustration, think of the following situation. Let the finite dictionary D consist of the alphabetical letters and punctuation symbols in English together with some technical symbols commonly used in scientific writings. By the proof given in section 3, we know that we can obtain every sentence written in English (in the broad sense). For example, every line of Shakespeare's poems and every statement in physics, among other things. In particular, we have all the statements in physical sciences and all the statements in biological and social sciences. Likewise, we have all the statements which are derivable from Newton's physics, and all those which are true only in Einstein's physics. Now, if a world is characeterized by way of a set of statements, we may take all the statements in the currently accepted scientific theories as a depiction of our world. However, until the program of unified sciences is fully carried out, the consistency of the set of all scientific statements may be far from easy to prove. Hence, let us propose that scientific statements be thought of as expressing our "rational beliefs". (This is a pragmatical concept). We then tolerate the co-exsitence of scientific statements so far as the inconsistency is not explicitly shown. For instance, let Λ1, Λ2, Λ3,…, be, respectively, the set of scientific statements in physical science, biological science, social science and so on. Obviously, we want each ofΛi be a consistent class. Let us call it the intra-consistency. But the consistency of the union set
∞
U Λi
i=1
call it inter-consistency, may be quite questionable. Hence, instead of making maximal consistency extension in the way described last section, let us make such an extension to eachΛi with respect to the statements in that science (there are again denumerably many). Then, a possible world can be represented as
∞
(H) U λi
i=1
whereλi Λi for every i in the list. For example, our world will be characterized by the union of the sets of all currently accepted scientific statements.
Λi for every i in the list. For example, our world will be characterized by the union of the sets of all currently accepted scientific statements.
7.Some of the consequences and refinements.
∞
U Λi
i=1
call it inter-consistency, may be quite questionable. Hence, instead of making maximal consistency extension in the way described last section, let us make such an extension to eachΛi with respect to the statements in that science (there are again denumerably many). Then, a possible world can be represented as
∞
(H) U λi
i=1
whereλi
 Λi for every i in the list. For example, our world will be characterized by the union of the sets of all currently accepted scientific statements.
Λi for every i in the list. For example, our world will be characterized by the union of the sets of all currently accepted scientific statements.7.Some of the consequences and refinements.
As we mentioned at the beginning of this discussion, philosophers use the concept "possible world" from time to time. Let us briefly indicate some of the issues which might be explained in the light of our discussion, and thus outline a refinement to our syntactical notion of possible world.
(1)The concept "validity" when applying to an argument : We frequently maintain that an argument is valid of and only if the conclusion would be true, should the premises all be true. We may translate this in our terminology as saying that for every set Γi of statements which is thought to depict a possible world, if the premises are inΓi, then the conclusion must also be inΓi.
This interpretation, however, brings us a problem. It is easy to see that there are some setΓi which contain the premises of a valid argument, but does not certain the conclusion of it. This indicates that if we want to preserve our interpretation about validity, then we have to make some adjustment in our definition of possible world. This can be easily accomplished in the following way.
LetΓ1, Γ2,… be an enumeration of all the maximally consistent classes of statements as we mentioned above. Let Ω1, Ω2,…, be an enumeration of the elements of all the power sets ofΓ1, Γ2,…(Clearly there is such an enumeration). Define an L-maximal setΩi* ofΩi as follows: (i) Ωi  Ωi*, and (ii) for every statement S1, S2,…, Sk
Ωi*, and (ii) for every statement S1, S2,…, Sk Ωi, if S1, S2,…, Sk entail some statement Sk+1, then Sk+1
Ωi, if S1, S2,…, Sk entail some statement Sk+1, then Sk+1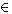 Ωi*. Obviously, eachΩi* has the following additional properties: (iii)EachΩi* is a consistent set. (iv) Every analytically true statement belongs to eachΩi*; and (v) no analytically false statements belong to anyΩi*. We will say that each suchΩi* characterizes a possible world Wi, and callΩi* the characteristic set of Wi. Under this definition, every characteristic set is L-maximal.
Ωi*. Obviously, eachΩi* has the following additional properties: (iii)EachΩi* is a consistent set. (iv) Every analytically true statement belongs to eachΩi*; and (v) no analytically false statements belong to anyΩi*. We will say that each suchΩi* characterizes a possible world Wi, and callΩi* the characteristic set of Wi. Under this definition, every characteristic set is L-maximal.
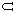 Ωi*, and (ii) for every statement S1, S2,…, Sk
Ωi*, and (ii) for every statement S1, S2,…, Sk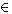 Ωi, if S1, S2,…, Sk entail some statement Sk+1, then Sk+1
Ωi, if S1, S2,…, Sk entail some statement Sk+1, then Sk+1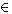 Ωi*. Obviously, eachΩi* has the following additional properties: (iii)EachΩi* is a consistent set. (iv) Every analytically true statement belongs to eachΩi*; and (v) no analytically false statements belong to anyΩi*. We will say that each suchΩi* characterizes a possible world Wi, and callΩi* the characteristic set of Wi. Under this definition, every characteristic set is L-maximal.
Ωi*. Obviously, eachΩi* has the following additional properties: (iii)EachΩi* is a consistent set. (iv) Every analytically true statement belongs to eachΩi*; and (v) no analytically false statements belong to anyΩi*. We will say that each suchΩi* characterizes a possible world Wi, and callΩi* the characteristic set of Wi. Under this definition, every characteristic set is L-maximal.After this refinement, it is clear that should the premises of a valid argument be inΩI*, then the conclusion of that argument would also be inΩi*.
This and other similar considerations lead us to think of those non-L-maximal sets as representing not bona fide possible worlds, but rather propotypes of possible worlds. These prototypes can be regarded as in an unstable state which, when exposed to logic, are quickly extended to L-maximal (consistent) sets.
The "empty world" can also be thus regarded. But under our new definition, it contains every analytically true statement. And hence, no longer being "empty".
(2)Alethic modalities, that is, necessity and possibility: To say that it is necessary that p can be taken in our discussion as meaning that p is a member of every characteristic setΩI*. Likewise, that it is possible that p means that p is a member of some characteristic setΩj*. Again, it is obvious that we need to restrict our characteristic sets to those which are L-maximal.
(3)Counterfactual conditionals: Sometimes it is said that a statement of the following form:
(J) Allx are y.
is a lawlike statement if the following two conditions are satisfied:
(J) Allx are y.
is a lawlike statement if the following two conditions are satisfied:
(i)For all a, if a is an x, then it is a y; and
(ii)For all b which is not an x, if it were an x then it would be a y.
On the otherhand, if only (i) is satisfied, then the statement is not lawlike, but merely an accidental generalization.
On the otherhand, if only (i) is satisfied, then the statement is not lawlike, but merely an accidental generalization.
In our terminology, one way of rendering the counter-factual part of the above conditions is this:
LetΩi* be the characteristic set of our world, for every characteristic setΩj*, whereΩi*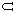 Ωj*, if
Ωj*, if
(K) 'b is an x'
is inΩj*, then
(L) 'b is a y'
is inΩj*, too. Or, if this is found to be too strong, we may follow the approach mentioned in last section.
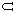 Ωj*, if
Ωj*, if(K) 'b is an x'
is inΩj*, then
(L) 'b is a y'
is inΩj*, too. Or, if this is found to be too strong, we may follow the approach mentioned in last section.
Let (J), or strictly speaking, the instantiation of (J), be in Λj (e.g., in the physico-scientific theory), where Δj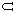 Ωi* (the characteristic set of our world). (J) is said to be law-like, if for everyΩm*, whereΔj
Ωi* (the characteristic set of our world). (J) is said to be law-like, if for everyΩm*, whereΔj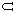 Ωm*, (L)
Ωm*, (L)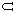 Ωm*provided that (K)
Ωm*provided that (K)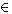 Ωm*
Ωm*
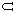 Ωi* (the characteristic set of our world). (J) is said to be law-like, if for everyΩm*, whereΔj
Ωi* (the characteristic set of our world). (J) is said to be law-like, if for everyΩm*, whereΔj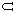 Ωm*, (L)
Ωm*, (L) Ωm*provided that (K)
Ωm*provided that (K) Ωm*
Ωm*
Another way of paraphrasing a counterfactual conditional is to say that for every characteristic setΩn* if the antecedent of the conditional is inΩn*, then the consequent of it is also inΩn*. This is a rather strong claim, because this seems to assume that all possible worlds, or at least certain aspects of all possible worlds, are subject to the same "natural laws", while the first interpretation we just gave entails only that similar worlds are subject to similar laws.
(4)In the light of our discussion, the scientific inquiry can be regarded as an effort to arrive at the characteristic set of our world, or to locate and relocate our world in a list of possible worlds. This effort could not be effectively done by a machine, if there should be infinitely many possible worlds. Hence, creative thinking and ingenuity are always indispansable in the scientific inquiry.
8.Postscript.
8.Postscript.
The discussion we have carried out so far is an outline rather than a complete theory. It cannot be a complete theory unless some other important problems are also considered. Among them: (1) the roles which individuals and the spatio-temporal coordination play in our theory, and (2) the expressive power of the language which is used to form all characteristic sets. How do we know, for example, that the language we use is so powerful that there are characteristic sets which can be formed in terms of other language but can not be formed by means of our language, and so on. However, since our discussion is already long, let us leave these problems to another occasion.
Hsiu-hwang Ho
Stanislaus State College
Hsiu-hwang Ho
Stanislaus State College